gwcc2p2

G.W. Coding Contest 2 P2: PC Part Picking

Kevin is building an awesome new PC and he needs to purchase components. The components are located at N different shops on a grid, and each shop has a distinct coordinate pair such that no shops share the same \(x\)-coordinate.

Kevin starts at \((0, 0)\), visits each shop, and ends at \((100, 100)\). He needs to visit the shops in an increasing order of \(x\)-coordinates. Given \(N\) distinct coordinate pairs for each shop \((a, b)\), \(\{0 < a, b < 100\}\), determine the shortest possible distance that Kevin needs to travel to reach every shop rounded down to the nearest integer.

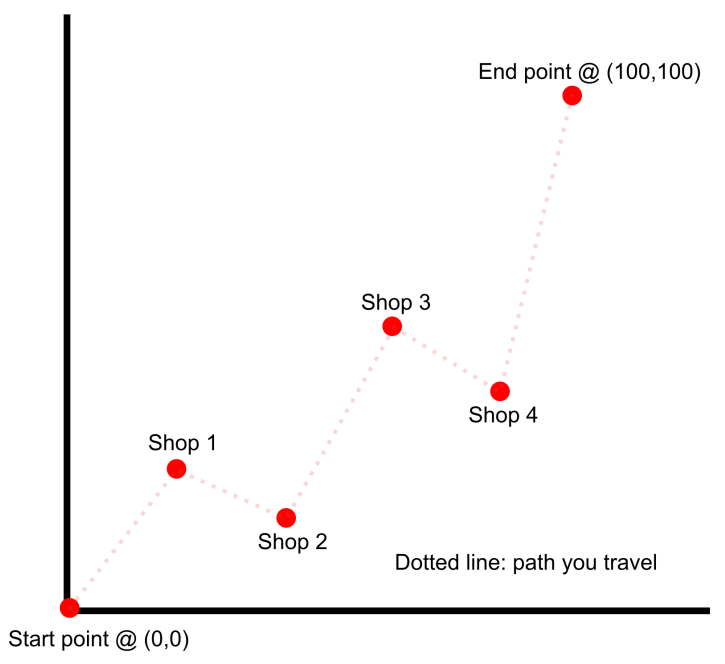
Note: The answer should be rounded down, intermediate calculations should always remain as decimals to maintain accuracy.

Input Specification:

The first line of input will contain \(N\), the number of shops Kevin needs to visit.

The next \(N\) lines will contain two integers, \(a\) and \(b\), seperated by a space, representing the \(x\) and \(y\) coordinates of each shop respectively.

Output Specification:

The output will consist of a single integer, the total distance Kevin must travel if he takes the shortest path.

TIME CONSTRAINT: 1s

Sample Input 1:

5
72 92
57 3
40 66
21 64
62 22

Sample Output 1:

271

Explanation for Sample Input 1:

Because Kevin needs to move from increasing \(x\) coordinate, we know the order of shops we must visit is \((21, 64)\), \((40, 66)\), \((57, 3)\), \((62, 22)\), \((72, 92)\). The shortest path from \((0, 0)\) to \((21, 64)\) is \(67.357256476196\). If we calculate the shortest path between each point in our order and sum them, it will result in our answer.