gwcc2p6

G.W. Coding Contest 2 P6: Hall Traffic

Samuel is getting tired of the hall traffic at Dr. G.W. Williams S.S when moving classes, so he decides to measure the average number of people in each hall after every period, on both floors. Each hall is labelled with a number increasing from 1, and some halls are connected to the other floors by stairs which go directly upwards (Stairs are considered as 0 average people). Starting from his class at hall \(A\), what is the least crowded pathing Samuel can use get to his class in hall \(B\)?

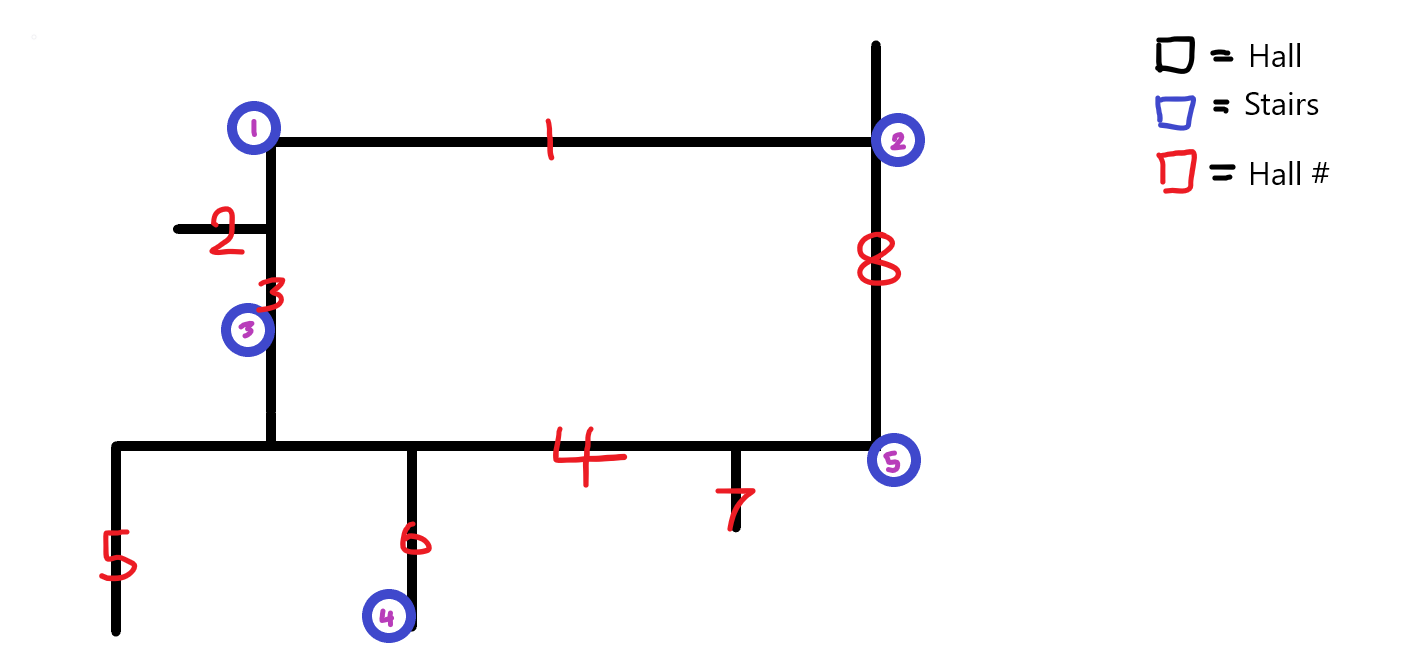
The hall and stair placements are formatted in the same manner as the diagram shown below, to pass through a hall in any capacity will incur it's cost. Stairs in the corners of halls are connected to both halls, meaning you do not need to incur the cost of the other hall to use the stairs.

Input Specification:

The first line will contains two integers, \(A\), the starting hall, and \(B\), the destination hall.

The next 12 lines will contain \(K\), the average number of people in each hall, for each respective hall \(\{1 \leq K \leq 2^{63}\). (i.e. line 2 is for hall 1, line 3 is for hall 2, etc.)

Output Specification:

Output the pathway Sam can take to minimize the traffic he must go through, each hallway should be seperated by a new line.

TIME CONSTRAINT: 1s

Floor 1:

Floor 2:

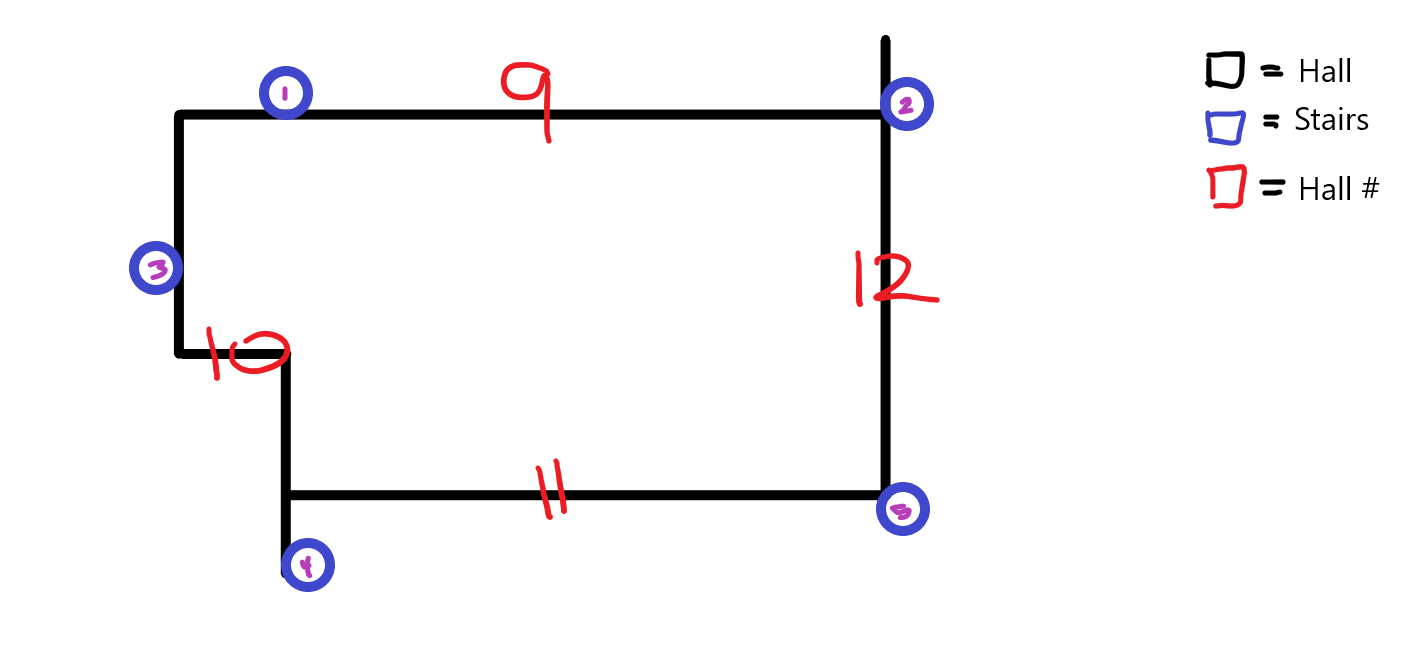
Note: The connections to stairs work in a mannner such that if any part of the hall is touching the stair, then that hall is connected to that stair. For example, hall 1, 3 and 9 are all the connections to stair 1.

Sample Input 1:

2 12
14
2
3
15
7
8
6
11
13
3
4
9

Sample Output 1:

2
3
10
11
12

Explanation for Sample Input 1:

We start at hall 2, meaning it must be included. The same applies to hall 12.
Next, we must move to hall 3, as it is the only connected hall.
Then, we can choose between either going to hall 1, hall 4, or taking the stairs. If we take hall 1 or 4 the cost incurred will outweigh if we go up the stairs and travel to our destination in every case.
Finally, we are at hall 10, and can either take the path 10 -> 9 -> 12 or 10 -> 11 -> 12. Because the cost to take hall 11 is less than the cost to take hall 9, we then take hall 11.

Sample Input 2:

1 9
62
11
83
39
75
64
35
60
22
35
5
67

Sample Output 2:

1
9